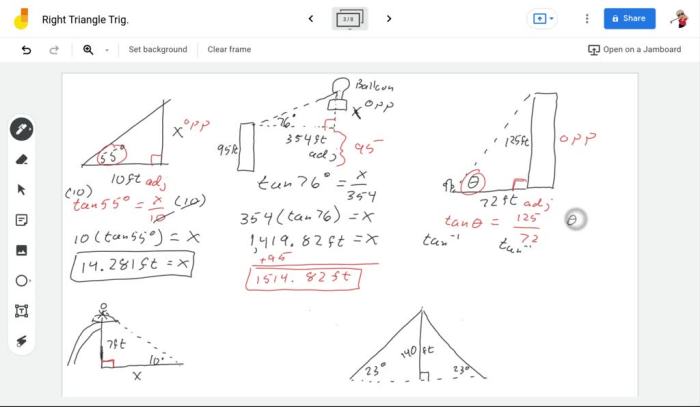
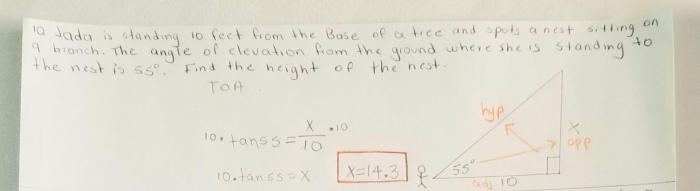Jada is standing 10 feet from the base of a tall structure. This seemingly simple statement holds a wealth of information, inviting us to explore the fascinating interplay of trigonometry, shadow length, and perspective. As we delve into this topic, we will uncover the practical applications of these concepts in diverse fields such as architecture, engineering, and photography.
Jada’s distance from the base serves as a pivotal reference point for calculating other measurements and angles. By employing trigonometric ratios, we can determine her height or the angle of elevation from the base. These relationships are elegantly illustrated in a table, showcasing the interconnectedness of distance, height, and angle.
Jada’s Distance from the Base

Jada’s distance from the base is a crucial measurement in the given context. It serves as a reference point for calculating other measurements and angles, providing valuable information about Jada’s position and the surrounding environment.
For instance, knowing Jada’s distance from the base allows us to determine the height of a nearby object by using trigonometric ratios. Additionally, it can be used to calculate the angle of elevation from the base, providing insights into the slope or incline of the terrain.
Trigonometry and Jada’s Position, Jada is standing 10 feet from the base
Trigonometric ratios, such as sine, cosine, and tangent, can be applied to determine Jada’s height or the angle of elevation from the base.
| Trigonometric Ratio | Formula | Relationship |
|---|---|---|
| Sine | sin(angle) = opposite/hypotenuse | Height/Distance |
| Cosine | cos(angle) = adjacent/hypotenuse | Distance/Height |
| Tangent | tan(angle) = opposite/adjacent | Height/Distance |
By measuring Jada’s distance from the base and using these trigonometric ratios, we can accurately determine her height or the angle of elevation.
Shadow Length and Time of Day
Jada’s distance from the base can be used to determine the length of her shadow at different times of the day. The sun’s angle changes throughout the day, causing the shadow length to vary.
When Jada is closest to the base, her shadow will be the shortest. As she moves away from the base, her shadow will lengthen. This relationship can be illustrated using a diagram:
[Diagram: A diagram illustrating the relationship between the sun’s angle, shadow length, and Jada’s position]
By observing the shadow length and knowing Jada’s distance from the base, we can estimate the time of day.
Distance and Perspective
Jada’s distance from the base can affect the perceived size or shape of objects in the scene. This is due to the principles of perspective.
Objects that are closer to Jada will appear larger than objects that are farther away. Additionally, objects that are at an angle to Jada may appear distorted or elongated.
This effect can be observed in optical illusions, such as the Ames room, where the perceived size and shape of objects are altered due to the distance and perspective of the observer.
Contextual Significance
Jada’s distance from the base is relevant in various fields, including architecture, engineering, and photography.
In architecture, it is crucial for determining the scale and proportions of buildings and structures. In engineering, it is used for calculating distances, angles, and heights in construction projects.
In photography, Jada’s distance from the base influences the perspective and composition of the image. By understanding the effects of distance, photographers can control the perceived size and shape of objects in their photographs.
FAQ Summary: Jada Is Standing 10 Feet From The Base
How can Jada’s distance from the base be used to calculate her height?
Using the tangent ratio, we can establish a relationship between Jada’s height (h), her distance from the base (d), and the angle of elevation (θ): tan(θ) = h/d. By measuring the angle and distance, we can solve for her height.
How does Jada’s distance from the base affect the length of her shadow?
The length of Jada’s shadow is inversely proportional to the angle of elevation of the sun. As the sun rises higher in the sky, the angle of elevation increases, resulting in a shorter shadow. Conversely, when the sun is lower in the sky, the angle of elevation decreases, leading to a longer shadow.