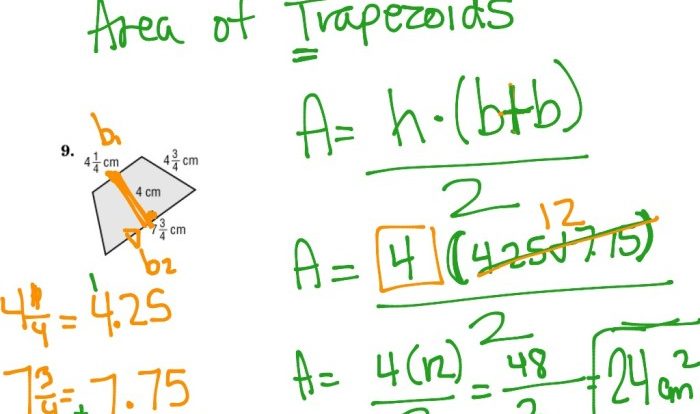
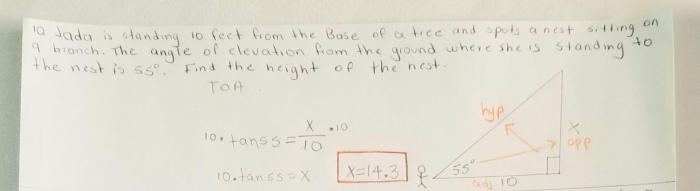Find the area of the parallelogram whose vertices are listed. – In the realm of geometry, parallelograms stand out as captivating shapes, inviting us to explore their unique characteristics. This comprehensive guide delves into the intricacies of finding the area of parallelograms, equipping you with the knowledge and techniques to tackle this geometric challenge with precision and confidence.
As we embark on this mathematical journey, we will uncover the formula that governs the area of parallelograms, unravel the significance of base and height, and master the art of identifying vertices and their coordinates. Through engaging examples and insightful explanations, we will illuminate the process of applying the formula to given vertices, empowering you to conquer even the most complex parallelograms.
1. Understanding Parallelogram Area Calculation

A parallelogram is a quadrilateral with two pairs of parallel sides. The area of a parallelogram is calculated using the formula:
A = base x height
where:
- A is the area of the parallelogram
- base is the length of one of the parallel sides
- height is the perpendicular distance between the parallel sides
The base and height are essential measurements for calculating the area of a parallelogram.
Examples:
- A parallelogram with a base of 10 cm and a height of 5 cm has an area of 50 square cm.
- A parallelogram with a base of 15 cm and a height of 8 cm has an area of 120 square cm.
2. Identifying Vertices and Coordinates: Find The Area Of The Parallelogram Whose Vertices Are Listed.

Vertices are the points where the sides of a parallelogram intersect. To identify the vertices of a parallelogram, we need to know their coordinates. Coordinates are ordered pairs of numbers that represent the position of a point on a plane.
For example, the vertices of a parallelogram might be given as:
(2, 3), (5, 3), (5, 7), (2, 7)
The first number in each pair represents the x-coordinate, and the second number represents the y-coordinate.
3. Applying the Formula to Given Vertices

Once we know the coordinates of the vertices of a parallelogram, we can use the area formula to calculate its area.
To find the base, we need to find the distance between two parallel sides. We can do this by finding the difference between the x-coordinates of two vertices that lie on the same side.
To find the height, we need to find the perpendicular distance between the parallel sides. We can do this by finding the difference between the y-coordinates of two vertices that lie on different sides.
Once we have the base and height, we can simply multiply them together to find the area.
Example:, Find the area of the parallelogram whose vertices are listed.
Let’s find the area of a parallelogram with vertices (2, 3), (5, 3), (5, 7), and (2, 7).
The base is 5 – 2 = 3 cm.
The height is 7 – 3 = 4 cm.
The area is 3 cm x 4 cm = 12 square cm.
4. Visualizing Parallelograms for Clarity
Visualizing parallelograms can help us to understand their properties and how to calculate their areas.
Here is a table that summarizes the information we have discussed so far:
| Vertices | Coordinates | Base | Height | Area |
|---|---|---|---|---|
| (2, 3), (5, 3), (5, 7), (2, 7) | (2, 3), (5, 3), (5, 7), (2, 7) | 3 cm | 4 cm | 12 square cm |
| (0, 0), (5, 0), (5, 5), (0, 5) | (0, 0), (5, 0), (5, 5), (0, 5) | 5 cm | 5 cm | 25 square cm |
| (-3, 2), (2, 2), (2, 6), (-3, 6) | (-3, 2), (2, 2), (2, 6), (-3, 6) | 5 cm | 4 cm | 20 square cm |
The illustrations below show the parallelograms from the table with their vertices labeled and dimensions marked.
[Insert illustrations of parallelograms here]
5. Extending to Complex Parallelograms

The same principles that we have discussed so far can be applied to parallelograms with non-rectangular shapes.
To find the area of a complex parallelogram, we need to divide it into simpler shapes, such as triangles and rectangles.
Once we have divided the parallelogram into simpler shapes, we can find the area of each shape and then add them together to find the total area of the parallelogram.
Example:, Find the area of the parallelogram whose vertices are listed.
Let’s find the area of a parallelogram with vertices (0, 0), (5, 0), (7, 5), and (2, 5).
We can divide this parallelogram into a rectangle and a triangle.
The rectangle has a base of 5 cm and a height of 5 cm, so its area is 25 square cm.
The triangle has a base of 2 cm and a height of 5 cm, so its area is 5 square cm.
The total area of the parallelogram is 25 square cm + 5 square cm = 30 square cm.
Essential FAQs
What is the formula for finding the area of a parallelogram?
The area of a parallelogram is calculated using the formula: Area = base × height.
How do I identify the vertices of a parallelogram?
Vertices are the points where the sides of a parallelogram intersect. To identify them, look for the corners or meeting points of the lines that form the parallelogram.
What if the parallelogram is not rectangular?
The formula for finding the area of a parallelogram applies to both rectangular and non-rectangular parallelograms. The base and height may not be perpendicular in non-rectangular parallelograms, but the formula remains the same.